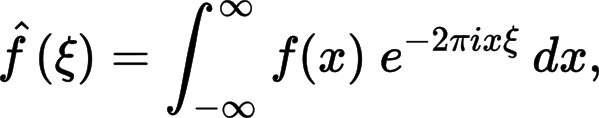Mathematical Information Retrieval (MathIR)
As part of the DFG-funded research project GI 1259/1-1
Methods and Tools to Advance the Retrieval of Mathematical Knowledge from Digital Libraries for Search-, Recommendation- and Assistance-Systems,
we investigate fundamental methods and tools for making mathematical knowledge accessible to information retrieval tools.
Achieving this goal requires methods to reliably extract mathematical knowledge from documents. In the domain of natural language processing (NLP), a number of well-established, general purpose text processing methods and tools exist that are applied to a text to enable domain specific extraction tasks. Similar to state-of-the-art text processing tools, such as the Stanford NLP toolkit, our research will determine how similar tools for processing mathematical language can be realized.
Our approach is to expand upon the concept of Mathematical Language Processing (MLP), a concept for which we have already demonstrated its feasibility when we presented it at the ACM SIGIR conference in 2016 (link to paper). In the context of this project, we expand upon our preliminary research to make the approach more effective and applicable for real world mathematical information retrieval applications. Specifically, the project has the following objectives:
- Identify mathematical formulae and expressions in documents, and reliably differentiate them from similar or neighboring structures.
- Perform type detection and tokenization of mathematical expressions.
- Extract the corresponding mathematical concepts from the tokenized mathematical formulae and expressions.
Our goal is enabling other scientists to use our methods and tools for mathematical language processing to tackle their own novel problems. We hope that MLP will continue to improve during this process, as was once the case for early NLP approaches.
A wide variety of applications would benefit from advancements to mathematical information retrieval. In the STEM disciplines, improvements could be made to academic literature search, literature recommendation, and even plagiarism prevention. Additionally, expert search or applications in pure mathematics, such as theorem search or definition lookup, would significantly benefit from our developments. Applications beyond STEM fields include the improvement of tutoring assistance tools, as well as patent search and enterprise search, which could become more valuable to companies if they integrate math-aware information retrieval methods.
RELATED PUBLICATIONS
2020
- Discovering Mathematical Objects of Interest – a Study of Mathematical Notations
A Greiner-Petter, M Schubotz, F Müller, C Breitinger, HS Cohl, A Aizawa, B Gipp
Proceedings of the Web Conference 2020 (WWW’20), April 20–24, 2020, Taipei, Taiwan
DOI: 10.1145/3366423.3380218 Preprint Core Rank A*
2019
- Improving Academic Plagiarism Detection for STEM Documents by Analyzing Mathematical Content and Citations
N Meuschke, V Stange, M Schubotz, M Kramer, B Gipp
Proceedings of the Annual International ACM/IEEE Joint Conference on Digital Libraries (JCDL)
DOI: 10.1109/JCDL.2019.00026 Preprint Core Rank A* - AnnoMath TeX- a Formula Identifier Annotation Recommender System for STEM Documents
P Scharpf, I Mackerracher, M Schubotz, J Beel, C Breitinger, B Gipp
Proceedings of the 13th ACM Conference on Recommender Systems 2019, Copenhagen, Denmark, September 16-20, 2019
DOI: 10.1145/3298689.3347042 Preprint Bibtex Homepage Core Rank B - Why Machines Cannot Learn Mathematics, Yet
A Greiner-Petter, T Ruas, M Schubotz, A Aizawa, W Grosky, B Gipp
4th Joint Workshop on Bibliometric-Enhanced Information Retrieval and Natural Language Processing for Digital Libraries co-located with the 42nd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval
PDF - Semantic Preserving Bijective Mappings for Expressions Involving Special Functions in Computer Algebra Systems and Document Preparation Systems
A Greiner-Petter, M Schubotz, HS Cohl, B Gipp
Aslib Journal of Information Management
DOI: 10.1108/AJIM-08-2018-0185 Preprint Bibtex - Towards Formula Concept Discovery and Recognition
P Scharpf, M Schubotz, HS Cohl, B Gipp
Proceedings of the 4th Joint Workshop on Bibliometric-Enhanced Information Retrieval and Natural Language Processing for Digital Libraries (BIRNDL 2019) co-located with the 42nd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Paris, France, July 25, 2019.
PDF Preprint Bibtex - Forms of Plagiarism in Digital Mathematical Libraries
M Schubotz, O Teschke, V Stange, N Meuschke, B Gipp
Proceedings International Conference on Intelligent Computer Mathematics
DOI: 10.1007/978-3-030-23250-4_18 Preprint
2018
- Improving the Representation and Conversion of Mathematical Formulae by Considering their Textual Context
M Schubotz, A Greiner-Petter, P Scharpf, N Meuschke, HS Cohl, B Gipp
Proceedings of the 18th ACM/IEEE on Joint Conference on Digital Libraries (JCDL)
DOI: 10.1145/3197026.3197058 Preprint Bibtex Core Rank A* - HyPlag: A Hybrid Approach to Academic Plagiarism Detection
N Meuschke, V Stange, M Schubotz, B Gipp
Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval
DOI: 10.1145/3209978.3210177 Preprint Bibtex Core Rank A*. - Automated Symbolic and Numerical Testing of DLMF Formulae Using Computer Algebra Systems
HS Cohl, A Greiner-Petter, M Schubotz
Intelligent Computer Mathematics – 11th International Conference, CICM 2018, Hagenberg, Austria, August 13-17, 2018, Proceedings
DOI: 10.1007/978-3-319-96812-4_4 Bibtex - MathTools: An open API for convenient MathML handling
A Greiner-Petter, M Schubotz, HS Cohl, B Gipp
Intelligent Computer Mathematics – 11th International Conference, CICM 2018, Hagenberg, Austria, August 13-17, 2018, Proceedings
DOI: 10.1007/978-3-319-96812-4_9 Bibtex - Towards Formula Translation Using Recursive Neural Networks
F Petersen, M Schubotz, B Gipp
Proceedings of the 11th Conference on Intelligent Computer Mathematics (CICM)
PDF Preprint Bibtex - Representing Mathematical Formulae in Content MathML Using Wikidata
P Scharpf, M Schubotz, B Gipp
Proceedings of the 3rd joint workshop on bibliometric-enhanced information retrieval and natural language processing for digital libraries (BIRNDL 2018) co-located with the 41st international ACM SIGIR conference on research and development in information retrieval (SIGIR 2018), ann arbor, USA, july 12, 2018.
PDF Preprint Bibtex - Generating OpenMath Content Dictionaries from Wikidata
M Schubotz
Joint Proceedings of the CME-EI, FMM, CAAT, FVPS, M3SRD, OpenMath Workshops, Doctoral Program and Work in Progress at the Conference on Intelligent Computer Mathematics 2018 co-located with the 11th Conference on Intelligent Computer Mathematics (CICM 2018)
DOI: 10.5281/zenodo.1409946 Preprint - Mathematische Formeln in Wikipedia
M Schubotz
Beiträge zum Mathematikunterricht 2018
DOI: 10.17877/de290r-19676 Preprint Bibtex - Introducing MathQA – a Math-Aware Question Answering System
M Schubotz, P Scharpf, K Dudhat, Y Nagar, F Hamborg, B Gipp
Proceedings of the Annual International ACM/IEEE Joint Conference on Digital Libraries (JCDL), Workshop on Knowledge Discovery
DOI: 10.1108/IDD-06-2018-0022 Preprint Bibtex
MEDIA COVERAGE
Hats off to Philipp Scharpf for sucessfully defending his PhD
The GippLab team is delighted to share the news that [...]
ACL 2023 – Neural Machine Translation for Mathematical Formulae
Authors: Felix Petersen, Moritz Schubotz, Andre Greiner-Petter, Bela Gipp Contact: [...]
Wikipedia rolls out our research on providing semantic information for mathematical formulae
As of January 9, Wikipedia allows semantically enhancing mathematical formulae [...]
New DFG Project about math retrieval
The DFG, Germany’s organization for research funding, has awarded our [...]
Improved math rendering in Wikipedia
Wikipedia is using a new approach for rendering mathematical formulae [...]
CitePlag on public radio
The national public radio broadcasters Deutschlandfunk and Deutschlandradio Kultur covered our collaborative research on [...]
